Yet Another XOR Tree Problem

Subtask 1:
Any bruteforce solution should pass.

Subtask 2:
In each $query(U, V)$, treat node $U$ as the root node of the tree. Run a BFS/DFS from node $U$ and track the nodes that lie on the simple path between node $U$ and node $V$. You can do it by managing a $par[]$ array, where $par[i] = immediate\space parent\space of\space node\space i$. You should also calculate $F(U, i)$ for all node $i$ while running BFS/DFS. The rest is for the solver to solve.

Subtask 3:
If you’re not familiar with finding maximum $K \oplus A_i$​ using Trie data structure, read this at first.

Let’s take an arbitrary node as the root of the tree. In the below example, we’ll treat node $1$ as the root node.

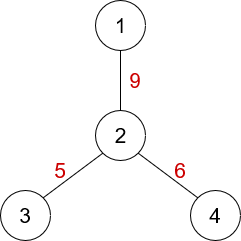
The weights of the edges are written in red colour. Here, $F(1, 4) = 9\oplus 6, \space F(1, 3) = 9\oplus 5$. So, $F(1,4) \oplus F(1,3) = 9\oplus 6\oplus 9\oplus 5 = 6 \oplus 5 = 3$, which is clearly the value of $F(4, 3)$. That is to say, we can write $F(U, V)$ as $F(root, U) \oplus F(root, V)$.

Let, the Lowest Common Ancestor (LCA) of node $U$ and node $V$ is node $L$. Now in queries, we can split the $query(U, V)$ queries into two separate queries: $query(L, U, F(root, U))$ and $query(L, V, F(root, U))$, where $query(x, u, k)$ means the maximum value of $k\oplus F(root, i)$ such that node $i$ lies on the simple path connecting node $x$ and node $u$; $x$ is node $u$ or any ancestor of node $u$. The maximum of these two splitted queries will be our desired answer for the real query.

To answer $query(x, u, k)$, we need to precalculate $F(root, u)$ for all node $u$ at first. After that, we can build a trie only using the values of $F(root, j)$, where $j$ is node $u$ or any ancestor of node $u$. Then it comes down to the normal trie problem stated at the beginning of the editorial (subtask 3). To ensure that we don’t search in a trie node created by only the ancestors of node $x$, we may track the maximum dfs discovery time in trie nodes or do similar kinds of things.

As building trie using the values of $F(root, j)$ for each node $u$ will be a huge memory-consuming task, we need to use Persistent Trie data structure.

This problem can also be solved using a normal Trie data structure by answering the queries offline. The above concept is helpful in this approach too.

Setter’s Sol: https://pastebin.com/Xdn7SrDD